摘要:筛选重点专利是专利分析的重要工作内容,需要采用既准确又便捷的重点专利筛选模型。文章从选择构建模型所采用的指标出发,对指标进行修正以提高其可获得性和代表性;随后提出以单个指标数值与指标中位数相减的指标处理方法,提升不同专利之间的差异性;最后提出构建标准尺度的指标整合方法,从而统一指标量纲和数量级,提升了计算专利价值常用的权重系数线性加和法的可操作性,并为指标扩展预留空间。根据实践验证结果,该重点专利筛选模型能够从高噪音专利样本中快速、客观地筛选出重点专利,具有良好的通用性和灵活性。
关键词:专利分析;重点专利;专利筛选模型
作者简介:王铮(1985—),男,河北保定人,硕士,高级知识产权师,研究方向:知识产权分析运用。
基于专利评价指标的分析方法是传统专利分析方法的延伸,能够从多维度探究专利数据背后所蕴含的丰富信息[1]。该方法的实施依赖于对重点专利的有效筛选。此处所称重点专利,指的是综合考虑专利的技术、经济和法律属性,能够体现专利对于其所属技术领域的引领性、能够反映其申请人的专利布局意图、在业界获得广泛关注的专利。
专利分析师希望既准确又便捷地筛选重点专利,但是在实践操作中,增加指标种类以提高模型精度往往伴随着工作量的巨大增加,并且受限于专利数据库收录不全面,或者指标需要经过计算方可用于上述模型中,造成个别指标难以方便获取。另一方面,专利分析师需要快速地从海量数据中筛选出重点专利,以期尽快为后续工作指明重点研究方向并缩短工期。因此,希望重点专利筛选模型在保证可靠性的基础上能够进一步实现较高的自动化程度。
本文对重点专利模型展开研究,通过同时对专利价值的指标选取和计算方法进行优化,从而提供一种兼顾精度与速度的改进的模型体系。
一、指标的选择
现有技术中筛选重点专利多采用指标权重线性加和法,计算公式如式(1)所示[2]:

此方法的基本原理是,将各指标的值(Ci)与其权重(Ai)相乘,各乘积加和以算出分值P作为专利价值评分,P值越大则专利越重要。
由此可见,建立重点专利筛选模型的第一步是选择适宜的体现专利价值的指标。业界对此已有研究[3-5] ,但这些指标的获取和应用往往有着严苛的适用条件,难以直接应用于模型计算之中。本文旨在提供一种兼顾精度与速度的改进的模型体系,对于指标的选择和计算处理应满足以下三个条件:
(1)单个指标定量可算:指标数据可从专利数据库导出数据中直接获取或仅需简单计算,避免过多人工参与以提高效率。
(2)指标取值差异 明显:对指标数据进行预处理,以使重点专利与非重点专利的差异更加明显。
(3)不同指标量级一致:对多个指标的量纲和数量级进行归一化处理,使之可以直接线性加和,确保模型的可操作性,保持引入更多指标的灵活性。
以之为前提,进一步考虑专利的本质属性,则指标优选覆盖技术、法律和商业这三个维度。进一步地,与针对特定技术点的学术研究不同,对于常规的基于大数据的专利分析,排斥需要通过复杂计算方可获得数据的指标;另外,专利在统计方面的另一个特点是存在“专利家族”①的概念,对于特定的指标而言,以“专利家族”为对象还是以“单件专利”为对象,会对该指标的取值造成影响,进而引入了额外的计算量乃至造成客观上无法计算的局面,故尽量降低额外的计算量也是筛选指标时的考虑因素。
基于上述考虑,从指标对于专利的代表性、指标数据获取难易等角度出发,本文选取被引用次数、引用次数、权利要求项数和家族成员数四个指标作为基本指标,并对其进行修正,参见表 1.

被引用次数是可以从数据库中直接导出的指标②,是反映专利技术价值的重要指标。需要修正的是,第三人引用 ③受到语言限制、数据库信息来源等的影响,导致同一专利家族的不同成员单独的被引用次数可能不同,因此应当采用专利家族总的被引用次数来统计。被申请人④主动引用的文献显然与其发明的技术具有密切关联,故引用次数的技术代表性较强,该指标同样可从数据库中直接导出,其同样采用专利家族总的引用次数来统计。
权利要求项数一般可从市面上主流数据库直接导出⑤,代表着申请人所请求保护和被批准予以保护的技术方案数量,是申请人和专利行政机关对该专利态度的直接体现,代表了专利的法律属性。对于不同家族成员的权利要求项数分歧,可以以家族最早授权成员为准;家族无授权则以最早公开成员为准,或以分析目标地域的家族成员为准。
专利家族成员数反映了申请人的专利布局地域态势,是专利经济属性的代表。该指标一般可从市面上主流数据库直接导出,只是对于同一申请号下各公开版本不重复计数。
除了上述四个指标外,还可以考虑诸如申请人/发明人数(技术属性)、专利权维持时间与专利授权周期(法律属性)、质押许可诉讼次数(市场属性)等,但其难点在于数据库是否准确完整地收录了相关信息,包括申请人变更情况、各成员授权情况、质押许可诉讼情况等,并且这些数据需要经过一定的计算方可转化为模型中所用的指标数据, 与本文“避免过多人工参与以提高效率”的宗旨相偏离。这些指标以及其他任何类似指标,尽管并非优选,但在条件允许的情况下同样可以纳入本文的模型之中,并且具有实际的可操作性,这是本文模型的优点所在,不同指标的整合与统一方法是后文研究的内容。
二、指标的处理
对于一个专利样本集合,每个专利均以若干指标为标准进行量化取值,即专利价值;对于每一个指标,希望通过一定的数学处理来凸显其与整体趋势的差异性,从而进一步提高模型的精度。
一种操作思路是,将一个指标在特定专利上的取值(下称特定值)与该指标在全部专利样本上的“趋势值”相减,如式(2)所示:
指标计算值 =指标特定值 - 样本中该指标的“趋势值”(2)
特定值与趋势值接近,则结果接近0.减弱乃至消除该指标对于该专利价值的影响;特定值大于趋势值,则结果为正,差异越大则正值越大;特定值小于趋势值则结果为负,与正值的情况产生显著区分,进一步拉低“低下”专利指标对于专利价值的影响。另外,从量纲上讲,减法不改变量纲(不存在除法处理后量纲为“1”的情况),以便在后续处理中实现不同类型和不同数量级的专利指标的整合。
那么问题聚焦于对于“趋势值”的选择。平均值是常见的反映样本整体情况的指标,但是对于重点专利筛选模型而言可能并不适宜。图1展示了专利样本 ⑥中各专利对应表1各指标的分布情况:
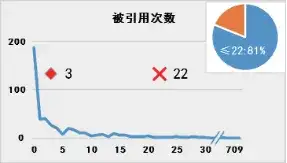
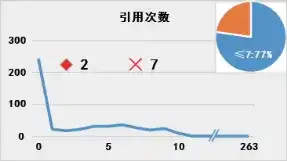
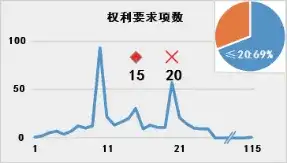
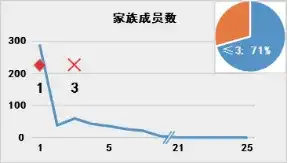
图1 专利数量(纵轴)相对于专利指标值(横轴)的分布
(注:菱形◇表示中位数,叉号× 表示平均数;右上角饼图中百分比表示指标值在平均数以下专利占比)
由图可见,表1所示指标的专利数量分布存在明显的特征:专利数量并非随指标值呈现正态分布,而是存在明显的聚集性,并且这种聚集性在指标数值的低位更加明显。聚集性是基于专利数量的累积而展现的,适宜的“趋势值”也应当反映出这种数量的集中。
采用平均值作为“趋势值”是不适宜的。图1中各指标特定值在平均值以下的专利占比均超过2/3.以“被引用次数”为例,被引用次数在平均值22次以下的专利高达81%,因此高被引专利属于稀有的“黑天鹅”,以平均值作为“趋势值”并不一定影响这些“黑天鹅”对于专利价值得分的贡献趋势,但是对于特定值位于平均数与中位数之间的、具有一定潜力的专利而言,依照式(2),则其对于专利价值得分的贡献为负值,即完全否定了这些专利的贡献,而其中不乏具有重要价值的周边专利。特别是对于聚集性较为分散的特征如“权利要求项数”而言,以一篇18项权利要求的专利为例,其与中位数15项的差距为3.该专利的权利要求项数已经超过了过半数的样本,则“3”这个正值反映出该专利相对于“普罗大众”而言存在一定优势;如果以平均数20为准,则“-2”的结果是将该专利完全归入“普罗大众”之中。单个指标无法对处于临界值的专利进行有效筛选,则多个专利指标组合起来会进一步放大这种偏差,最终导致以平均数为“趋势值”的专利价值得分只能区分最佳者与最差者,颗粒度过于粗糙,无法用于建立高精度模型。
相对于平均数而言,中位数将是一个更适宜的“趋势值”,它可以弥补平均数在偏态分布中的不足之处[6]。图1中示出各指标的中位数(菱形◇) 与平均数(叉号×)在专利数量分布中的位置,可见中位数与专利密集聚集的分布数量更加接近,以之为“趋势值”可以将绝大部分专利与特征值较为突出的专利区分开来,并将这种差异放大。基于此可将式(2)进一步修正为式(3):
指标计算值=指标特定值 - 样本中该指标的中位数(3)
以“被引用次数”为例,样本中绝大多数专利家族被引次数在中位数3次以下,则对于仅被引用一两次的低被引专利而言,其指标计算值为负数,从而拉低专利价值得分;被引用次数达到700余次的高被引专利,其指标计算值为正,并且其对专利价值得分的贡献可视为“增加”了相对于低被引专利的“负数”的绝对值,即起到放大效果。
值得一提的是,中位数在Excel、PowerBI中均有对应函数可以直接计算得出,方便分析人员进行数据处理。
三、指标的整合
通过前文的分析,确定了可以作为重点专利筛选模型所用的指标及单个指标的处理方法,接下来的问题是如何将多个指标组合起来以获得重点专利的分值。
式(3)在实际操作 中存在两个问题。一是不同的指标其量纲往往不同,例如权利要求数为“项”,而被引用次数为“次”,不同量纲的值直接加和是不合理的,并且这种不合理也无法通过无量纲的系数来修正。二是不同指标的数值的数量级可能存在极大差异,例如被引用次数可能高达几百次,而家族成员数则不超过50.指标值直接加和显然会导致“多指标体系”明显偏向于绝对值最高的指标,从而沦为“单指标体系”。理论上确实可以通过对不同的指标提供不同的权重系数来平衡各指标绝对值数量级的差异,但这违背了权重系数“用来平衡不同指标对总分值贡献程度”的基本用途,变成了对于单个指标自身取值的调整,并且不同的专利样本其绝对值最大的指标并不固定(尽管多为被引用次数)、最大者的数值亦不固定,实际上也不可能提供具有普适性的权重系数。
为了解决上述问题,以使模型具有良好的可操作性(特别是提高其自动化程度),需要构建一个“尺度”,其在逻辑上能够衡量在特定指标上单篇专利取值相对于样本整体所处的位置,即以“相对值”替代“绝对值”,来消除量纲和数量级(量级)的差异,同时其应当可以通过相对简单的计算实现、确保可操作性。
对于特定指标分析其数据构成,可以绘制出图 2:
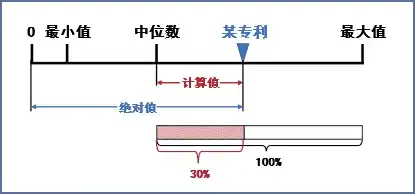
图2 特定指标的数据构成
基于某专利(倒三角▽)被引用次数的绝对值,以及样本的中位数,根据式(3)可以得出其计算值。同理,样本中被引用次数最大的专利亦可得出其“最大值”。该“最大值”显然是图中从中位数到最大值之间的一段“距离”,将其视作100%,那么某专利的计算值相当于“占据”了该“100%”中的一定比例(例如30%)。推而广之,对于样本中绝对值超过中位数的专利而言,其计算值都可以折算为以最大计算值为100%的相对份额,显然该份额的最小值是0%、最大值是100%⑦,其公式可以写作式(4):
指标相对值=(特定值 - 中位数)÷(最大特定值 - 中位数)×100% (4)
式(4)中,首先是通过将相同指标的计算值与最大计算值相除而将结果量纲归一,其次是将离散的计算值按照统一尺度折算为百分比,从而消除了不同指标的数量级的差异。基于此,可以对式(4)进行修改而得到式(5):
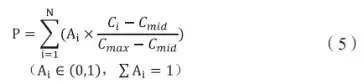
式(5)中,Ci是某专利的第i个指标的绝对值,Cmid、Cmax、Ai分别代表样本中第i个指标的中位数和最大值及其权重,对于N个指标线性加和算得分值P即专利价值。
对于权重系数Ai,其总和为1.意味着将全部用于计算的指标视为一个整体,利用取值范围为(0.1 )的权重系数调整各指标对于P值的贡献度,使得权重系数不再受到指标在专利样本中实际数值范围等变化因素的影响。
结合前文确定的四个指标:被引用次数、引用次数、权利要求项数和专利家族成员数,可以计算每一篇专利的分值,分值高者认为更加重要。基于式(5)的一个显著优点在于,可以根据实际情况灵活地增删指标,例如本文基于获得难度而忽略了专利权维持时间、专利授权周期等指标,如果这些指标的数据可以获得,则依然可以将其纳入式(5)中,进一步提高P值的客观性。
四、验证与讨论
作为验证,根据式(5)计算专利样本中各专利的专利价值,取其前十名列于表2中 ⑧。需要说明的是,本文未对专利样本进行人工阅读去噪,目的在于检验模型是否可以适用于对高噪音样本中重点专利的快速筛选。
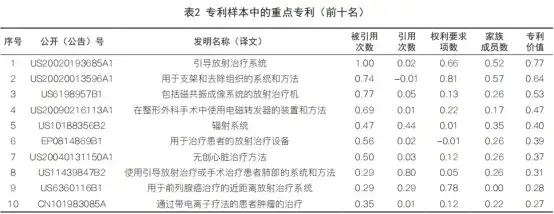
排名第一的US20020193685A1和第二的US2 0020013596A1均是美国瓦里安(VARIAN)的专利,其对应家族分别被引用700余次和500余次,并在美国、加拿大、澳大利亚、欧洲、日本等进行布局,两者属于同一技术路径,代表了该申请人在放疗图像引导方向的技术方向。
排名第五的US10188356B2同样是美国瓦里安的专利,其涉及同轴共面型图像引导放疗设备。该专利属于“集大成者”,是该申请人在技术发展早期为了抢占市场而布局的关键专利,尽管该专利被引用次数较低,但是其基于美国信息披露声明(Information Disclosure Statement,IDS)制度而披露了大量相关专利,专利引用次数高,进而推高了专利价值评分。
排 名 第 六 的EP0814869B1是 英 国 医 科 达(ELEKTA)的专利,其提供一种同轴共面型CT引导直线加速器,采用“宽射束”的射线束使患者支架至少部分地容纳在治疗装置,从而缩小设备体积并提高治疗精度。该专利在美、日、欧(英、德)进行布局,代表了该类型设备的发展趋势和该申请人的技术路线。
其他专利不再逐一分析。总结可见,利用式(5)确实可以筛选出专利样本技术领域中重要申请人的重要专利,尽管这些专利在各个指标上的特点各异,但式(5)能够对专利的价值进行综合性的评价,使结果更加客观,避免了单一指标绝对值过高而“掩盖”其他重点专利的情况;相关数据获得容易、计算处理简单,具有良好的操作性。
五、结语
利用本文的重点专利筛选模型,能够快速、客观地筛选出专利样本中的重点专利。该模型具有良好的通用性和灵活性,不受专利样本技术领域或其他因素的限制,在任何场景下均可适用,根据数据源情况还可以自由地增加专利指标,同时提供可以人工调整的权重系数以实现对于模型的微调,从而进一步提高模型精度。
特别值得一提的是,随着Microsoft PowerBI等基于大数据的商业情报分析软件(BI软件)在专利分析中的应用,通过将本文的模型嵌入到BI软件的数据模型之中,可实现重点专利筛选结果与专利数据库导出数据(即原始数据)的耦合,方便指标数据的获取,以及实现重点专利与其他专利因素(例如地域、时间等)的耦合,提升分析数据的深度和广度,有助于提升专利分析效率和提高专利分析质量。
(致 谢: 衷 心 感 谢 唐 跃 强 老 师 对 本 文 的指导。)
注释:
① 为了方便理解,本文采用德温特定义的简单专利家族,即优先权完全一致的各成员构成的专利家族。
② 笔者以智慧芽 Ⅲ专利数据库为例,其导出项包括“简单同族被引用专利总数”。
③ 第三人的引用泛指在后专利申请人以外的组织机构对于在前专利的引用,例如在专利实审、无效、诉讼阶段被审查员(合议组)、法庭、相关当事人引用。显然这些引用的目的与证明技术事实密切相关。
④ 专利授权后,申请人被称为专利权人。本文统一采用申请人这一称谓。
⑤ 智慧芽 Ⅲ仅对高级用户开放导出权利要求项数的功能,但是可以通过导出的权利要求文本简单地计算出该指标。
⑥ 此处笔者采用大型医疗设备领域的相关数据,检索数据库为智慧芽™,检索时间为2023年 4月。
⑦ 如前分析,对于专利的特定指标绝对值小于中位数的情况,该指标绝对值为负,亦可折算为相对100%的“负数份额”,视为该指标对该专利价值的贡献为负。
⑧ 各指标权重系数为:被引用次数0.6、引用次数0.2、权利要求项数0.1、专利家族成员数0.1.
参考文献:
[1] 国家知识产权局学术委员会. 专利分析实务手册[M]. 第 2版. 北京: 知识产权出版社, 2021:234.
[2] 马天旗. 专利分析:方法、图表解读与情报挖掘[M]. 第 1版. 北京: 知识产权出版社, 2015:164.
[3] Lanjouw J O, Schankerman M. The quality of ideas: measuring innovation with multiple indicators[J]. NBER Working Papers, 1999:1-35.
[4] Lanjouw J O, Schankerman M . Patent Quality and Research Productivity: Measuring Innovation with Multiple Indicators[J]. Economic Journal, 2004(114):441-465.
[5] Mariagrazia S, Dernis H, Criscuolo C. Measuring patent quality: Indicators of technological and economic value[J]. OECD Science, Technology and Industry Working Papers, No.2013/03. 2013: 1-69.
[6]张吉吉. 平均数、中位数和众数的意义分别是什么? [EB/OL]. (2018-07-25) [2023-08-17]. https://www.zhihu.com/question/286260644.








